Oefentoets kennisbasis rekenen 10voordeleraar

Gegeven:

Leerlingen spelen een spelletje met de rekenmachine. Op het beeldscherm van de rekenmachine staat het getal ‘234275’. De leerkracht vraagt de leerlingen door middel van optellen of aftrekken de ‘4’ te veranderen in een ‘0’.

Sjors probeert dit te doen en krijgt ‘194275’ op zijn scherm.

Gevraagd:

Wat heeft Sjors gedaan?

A.  Hij heeft te veel afgetrokken.
B.  Hij heeft te veel opgeteld.
C.  Hij heeft te weinig afgetrokken.
D.  Hij heeft te weinig opgeteld.

Antwoord: A

Sjors had van het getal 234275 het getal 230275 moeten maken. Dan zou hij de 4 correct in een 0 hebben veranderd. Echter, Sjors krijgt 194275 op zijn scherm. Dit getal is veel kleiner dan 230275.
De conclusie is dat Sjors dus te veel heeft afgetrokken.

Je ziet hier het werk van Karin. Als zij breuken optelt, gebruikt zij consequent een foutieve strategie.

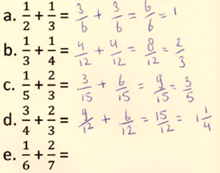
Gevraagd:

Welk antwoord geeft Karin bij opgave e, als zij dezelfde foutieve strategie toepast?

A. 3/7

B. 19/42

C. 1/2

Antwoord: C

Onderzoek welke fout Karin maakt. Het helpt om een aantal van haar berekeningen te bekijken.
Bij berekening a, maakt Karin de noemers correct gelijknamig. Ze kiest voor een noemer van 6. Hiervoor heeft ze bij de eerste breuk de teller en noemer met 3 vermenigvuldigd. Vervolgens zie je dat ze exact dezelfde berekening toepast bij de andere breuk. Ze vermenigvuldigt bij de breuk 1/3  de teller nu ook met 3. Dat is niet juist, ze had met 2 moeten vermenigvuldigen. Vervolgens telt ze de noemers bij elkaar op en vereenvoudigt ze het antwoord. Pas deze stappen nu toe op de som bij e.

De som is 1/6 + 2/7. Karin kiest voor een noemer van 42. Bij de eerste breuk zal ze de teller en noemer vermenigvuldigen met 7. Dit wordt 7/42. Bij de breuk 2/7 zal ze de teller óók met 7 vermenigvuldigen. De noemer is 42. De som wordt  7/42 + 14/42.  Dat is 21/42. Als ze vereenvoudigt, krijgt ze 1/2 als eindantwoord.

Gegeven:

Uit onderzoek blijkt dat in de periode 2000-2015 het aantal vissen van een vispopulatie met 15% afneemt. Onderzoekers vermoeden dat in de periode 2015-2020 sprake zal zijn van een afname van 20%. Op 1 januari 2010 werden 750.000 vissen geteld. De onderzoekers passen de berekening toe om het totaal aantal vissen op 1 januari 2020 te bepalen.

Gevraagd:

In welke berekening is het dalingspercentage correct toegepast?

A.  750.000 x 0,15 x 0,20

B.  750.000 x 0,15 x 0,80

C.  750.000 x 0,85 x 0,20

D.  750.000 x 0,85 x 0,80

Antwoord: D   

Je kunt dalingspercentages omzetten naar decimale getallen. In de periode 2000-2015 is het dalingspercentage 15%. Dat betekent dat er dan nog maar 100% – 15% = 85% van de vispopulatie over is.
Je kunt het percentage 85% omzetten naar een kommagetal. Je deelt door 100 en krijgt 0,85. Pas dezelfde strategie toe bij het dalingspercentage van 20%. Er is dan nog maar 100% – 20% = 80% van de vispopulatie over. Dat is 0,80. De beginhoeveelheid is 750.000 vissen. Je moet beide kommagetallen daarmee vermenigvuldigen. De correcte berekening is 750.000 x 0,85 x 0,80.

Gegeven:

In 2014 kost 1 m³ water in Brabant € 0,84 en in Zuid-Holland € 1,47.  Per persoon wordt in Nederlandse huishoudens ongeveer 125 liter water per dag gebruikt. Een gemiddeld Brabants gezin bestaat uit vier personen en een gemiddeld Zuid-Hollands gezin uit drie personen.

Wat is het verschil in waterverbruik kosten van een gemiddeld Brabants gezin en Zuid-Hollands gezin in 2014?

Gevraagd:

Hoe kun je dit uitrekenen?

A.  {(1,47 x 3) – (0,84  x 4)} x 0,125 x 365

B.  (1,47 – 0,84) x (4-3) x 125 : 1000 x 365

C.  (125 x 365) x (4-3) x (0,84-1,47) x 1000

Antwoord: A

Kijk eerst naar de gegevens per provincie. Zet de gegevens die bij elkaar horen, samen in de haakjes. In Zuid-Holland is de prijs € 1,47 en een gezin bestaat uit 3 personen. Daar maak je een keersom van.

Voor Brabant geldt een prijs van € 0,84 en een gezin bestaat uit 4 personen. Daar maak je ook een keersom van. Let erop dat deze prijzen gaan over 1 m³ water.
In de tekst staat dat er 125 liter water per persoon per dag wordt gebruikt. Reken dit om naar m³. Je deelt 125 door 1000 en krijgt 0,125. Omdat je wilt weten wat het verschil in waterverbruik is voor 2014 (één jaar), vermenigvuldig je met 365; het aantal dagen in een jaar.

Gegeven:

Op een blikje cola staat als maat aangegeven: 33 cl. Vier kinderen (11 jaar) krijgen de opdracht om dit volume om te rekenen naar cm³. De leerlingen doen de volgende uitspraken:

Anneke: “Het kunnen nooit kubieke centimeters worden, want het blikje is rond.”

Boutros: “33 cl is 33 cm³.”

Charlotte: “33 cl is 330 ml en dat is 330.000 cm³.”

Danielle: “33 cl is ongeveer een derde van een liter, dus het is 0,33 kubieke decimeter en dat is 330 kubieke centimeter.”

Gevraagd:

Welke leerling doet een wiskundig correcte uitspraak?

A.  Anneke

B.  Boutros

C.  Charlotte

D.  Danielle

Antwoord: D

Danielle heeft gelijk. 1 liter = 100 cl. Dus 33 cl is inderdaad ongeveer een derde van een liter. Als je
33 cl omrekent naar kubieke decimeter (dm³), bedenk je dat dm³ gelijk staat aan liter.
Om van centiliter naar liter te komen, deel je door 100. Je krijgt 0,33 kubieke decimeter.
Om vervolgens naar kubieke centimeter (cm³) te gaan, vermenigvuldig je met 1000. Je krijgt 330 cm³.

Waarom zijn de andere antwoorden fout?
Anneke heeft geen gelijk, want alle inhoudsmaten schrijf je in de vorm van een kubieke afmeting. Het gaat hier om een rond blikje waarvan je de inhoud kunt berekenen. Dat kunnen dus zeker kubieke centimeters worden (cm³).
Boutros heeft geen gelijk. Als je van 33 cl naar cm³ wilt rekenen, bedenk je dat cm³ hetzelfde is als een milliliter. Om van cl naar ml te komen, vermenigvuldig je met 10. Dat wordt 330 ml (dat is 330 cm³).
Charlotte heeft ook geen gelijk. Haar uitspraak dat 33 cl hetzelfde is als 330 ml is juist. Maar ml is hetzelfde als cm³. Het laatste deel van haar uitspraak is dus onjuist.

Gegeven:

In een sprookje verandert Pim in een reus. Alles aan hem is 9 keer zo lang geworden.

Gevraagd:

Hoeveel keer zo zwaar is hij geworden?

A.  9

B.  27

C.  81

D.  729

Antwoord: D

De zwaarte van Pim wordt bepaald door drie dimensies: lengte, breedte en diepte (dat is de dikte bij een persoon). Al deze afmetingen worden
9 keer zo lang. Dat betekent dat hij dus 9 x 9 x 9 = 729 keer zo zwaar wordt.

Gegeven:

Deze afbeelding toont een uitslag van een kubus. Je kan deze uitslag beschrijven als vier vierkanten op een rij met boven en onder die rij nog een extra vierkant. Op deze manier zijn nog andere uitslagen voor een kubus samen te stellen. Steeds vier vierkanten op een rij en boven en onder een vierkant. De uitslag is aan beide zijden blauw.

Gevraagd:

Hoeveel verschillende uitslagen, zoals hier omschreven, zijn er mogelijk?

Antwoord: 6

Gebruik het plaatje uit de som als voorbeeld. Dat is al een eerste manier om een uitslag te maken.
De vierkanten die je aan de rij plakt, liggen dan tegenover elkaar. De rij bestaat uit vier vierkanten (posities).
Bij ieder vierkant heb je de optie om boven en onder een extra vierkant te plakken.
Dat betekent dat je al 4 verschillende uitslagen hebt. Kijk of er nog meer opties zijn om een uitslag te maken. Je kunt ook een extra vierkant bij de eerste positie plakken en eentje bij de laatste. En je kunt een vierkant op de 2^e en 3^e positie plakken. Let erop dat het moet gaan om verschillende uitslagen. Er zijn niet meer opties om uitslagen te maken. In totaal zijn er dus 4 + 1 + 1 = 6 uitslagen mogelijk.

Gegeven:

In dit overzicht zie je een voorspelling van de groei van de grote steden van 2025 tot 2040.

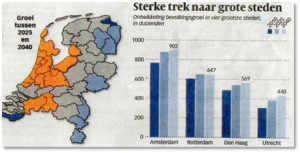
Gevraagd:

In welke stad is de voorspelling van de groei van 2025 tot 2040 procentueel gezien het grootst?

A.  Amsterdam

B.  Den Haag

C.  Rotterdam

D.  Utrecht

Antwoord: D

Voor deze som hoef je geen berekening te maken. Het is wel belangrijk dat je nauwkeurig de staafdiagrammen bekijkt. Je moet namelijk kijken naar de verschil van 2025 tot 2040 per stad.
Dat zijn steeds de twee meest rechter balkjes.
Bekijk bij welke stad het verschil in hoogte van die balkjes het grootst is. Dat is bij de stad Utrecht.

Gegeven:

Hieronder staat een steelbladdiagram van de lengtes (in cm) van enkele studenten uit PA1.

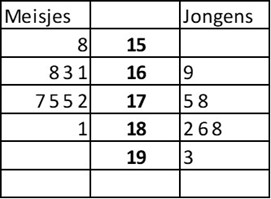
Gevraagd:

Hoe groot is de mediaan bij de lengte van de jongens?

A.  178

B.  180

C.  182

D.  184

Antwoord: C

Om de mediaan te berekenen, zet je de gegevens in een rij van klein naar groot. In het steelbladdiagram staat in de middelste kolom de tientallen/honderdtallen. En de getallen links en rechts daarvan geven de eenheden aan. Voor de lengte van de jongens ontstaat deze rij:

169 – 175 – 178 – 182 – 186 – 188 – 193

Om nu de mediaan te bepalen, kijk je welk getal in het midden staat van de rij. Dat is 182. Aan beide kanten staan er dan 3 getallen. Antwoord C is dus juist.